Codeforces Round 920 div3

 

Codeforces Round 920 (div 3)

 

 

Problem F

Square root trick,

You can use the square root trick to calculate prefix sums in n * sqrt(n).  Where you compute the prefix sums for each step size from 1 to sqrt(n).  Now anytime you have a query where d <= sqrt(n) it can be solved in O(1) with the precomputed prefix sum.  Else it will have sqrt(n) iterations in brute force looping through to get the value.

 

You do need two prefix sums because you have to create the ones that will give the answer for this specific problem.  Which is a little bit tricky to derive. 

Problem G

 

My approach was very bad for this problem.  You want to use a diagonal prefix sum and column-wise prefix sum.  But the thing is that implementation is very important.  If you try to pad by K to avoid where the diagonal is out of bounds you will end up with 10^5 by 10^5 matrix which is too large.  And if you pad by 1 for the diagonal prefix sum it is a difficult to deal with off by 1 situations.  The best method is to just create the prefix sums 0-indexed.  In that way you can deal with the edge cases with conditional logic. 

 

You can also just use one method and just flip the board to deal with the flipped orientations.

 

If you implement the secondary diagonal prefix sum, you have the following.

edge cases to consider is the diagonal you are removing going to exceed the left boundary, And also consider when you need to remove from the column-wise prefix sum.   And when you need to add from diagonal prefix sum.

 

Let's start with the easier aspect, the prefix sums.  so for this problem I need to construct a framework in my brain where I am treating edge cases.  The first edge case is that you are taking the columnwise,  Since you are adding this one, you need to add the columnwise sum, that is from top to bottom.  That is there are prefix sums from the 0th row to the Rth row.  Now you add this entire row, and then you may need to subtract the top if you are in a low enough row.  For example if K = 2, then when you are in row = 3, you need to subtract the prefix sum for this column at row - K - 1.  So basically if row - K - 1 >= 0 you are good, also you can increment K so you don't need the -1. 

 

For the diagonal sum you want to remove from current prefix sum.  I compute the prefix sums as secondary diagonals in the matrix. from top to bottom.  Now it is a little tricky cause sometimes the diagonal will be off the board, so how do you handle that?  You can deal with that case separately.  So if it does not extend off the board you know it will be at if c - K - 1 >= 0 (r, c - K - 1)  Now you remove that bit, and also you need to add the part above back which is at (r - K - 1, c), again if r - K - 1 >= 0

 

Now if c - K - 1 < 0 it is a little bit tricky cause the diagonal is extending off the board.  so you need to find where it will be on the board again.  You can notice the following pattern though,  as c becomes smaller with respect to K what happens is the following,  if c - K - 1 = 0 then you take mat[r][c - K - 1],  now this is mat[r][0], okay and then if c - K - 1 = -1, which means it is going off board by one, then you need to take mat[r-1][0] and if it is -2 then mat[r-2][0] and so on,  so basically you are taking r + c - K - 1, since if it is negative than you take that.  And you need to check this is greater than or equal to 0 as well. 

 

So I wouldn't say it is too difficult to deal with diagonal prefix sum and column-wise prefix sum and using that to track for one orientation of the area of damage.

 

But that is just one step to solving the problem.

 

You want to implement some property of the transformations so you can re-use the same algorithm each time.

 

 

You can think of these as discrete right triangles I think.  That is they are pixelated right triangles.    This is a right triangle that is limited to resolution of the grid.

 

The thing you can notice is that each image is a vertical/horizontal flip of just one of the shapes. 

 

 

The transformations that can be made to the geometry.

 

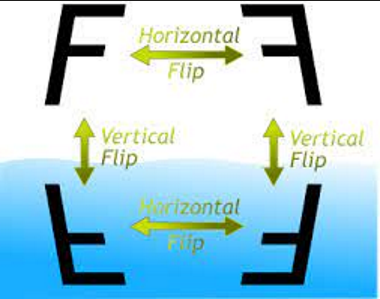
A vertical flip is a type of transformation applied to a two-dimensional array or matrix, such as an image, where each row of the matrix is inverted in order with respect to a horizontal axis.  In simpler terms, it's like flipping the matrix upside down.

 

A horizontal flip is a type of transformation applied to a two-dimensional arrays or matrix, such as an image, where each column of the matrix is inverted in order with respect to a vertical axis.  This is akin to filipping the matrix or image from left to right.

 

180 degrees rotation of matrix:

• A combination of horizontal then vertical flip (or vice versa), the result is that both the horizontal and vertical orders of the elements are reversed.
• This reversal of both orders is essentially what happens when you rotate the entire matrix or image by 180 degrees:  the top becomes the bottom, and the bottom becomes the top, the left becomes the right, and the right becomes the left.

 

 

 

If you look at the shape of the object, a discrete right triangle.  And you can see you can recreate the other orientations by just three transformations, that is vertical, horizontal and vertical + horizontal flips.  This is rather easy to encode.  Cause then you just need to perform the same shape scan through the matrix, but just flip all the elements of the matrix.  For example if you flipped vertical than that white shape would be actually computing the value for the vertically flipped blue image of it in the large matrix.